Hi everyone,

Little help required please.

I want to put LED indicators on my 1989 K100 project, I have connected them up and they just light up, they don't flash at all and a beep sound comes from what I think may be the relay ??

How do I make them flash.

I have the tail/brake light changed to LED no problem.

Any help would be much appreciated  

Andrew P

Inge has a mod that involves cutting one of the tracks in the relay. I tried to post the link but for some reason it would not load. Inge will probably post on it.
Regards Martin.

Have you installed ballast/balancing resistors for the new lights?

Without the load balancing resistors the circuit is a Short Circuit & will usually blow the fuse.
Led's have little or no resistance of their own.

HTH,

Troy

How to construct your own DIY LED relay but also includes pictures of where to cut the traces on the OEM flasher relay to adapt it to LEDs.

Tagaz

Are the resistors wired up in parallel to the LED bulbs or in series?

series

as a quick test use a jumper wire and connect the old incandescent bulbs in series with the leds.
should work as if you had the old lights installed with the additional leds functioning as well.
the circuit will see the led's as if they were just wire. that is they will not cause any additional resistance to the circuit.
but will draw current, so maybe a fuse will blow. or maybe not. as always YMMV.

i have a incandescent signal bulb & tail/stop bulb that i soldered some lengths of wire onto for use as test lights. 

hth,

troy

tagaz wrote:Have you installed ballast/balancing resistors for the new lights?

Without the load balancing resistors the circuit is a Short Circuit & will usually blow the fuse.
Led's have little or no resistance of their own.

HTH,

Troy

Hi Troy,

Tried to put resistors in and yes blew the fuse : (

I'm having another go at putting them inline ( saw it on youtube ) see if this works. If not I will post up some pictures to see if someone can help, electrics are not a strong point of mine

Andrew

robmack wrote:How to construct your own DIY LED relay but also includes pictures of where to cut the traces on the OEM flasher relay to adapt it to LEDs.

Hi Rob,

I did see this but its waaaayyyyyyyy out of my league 

Andrew

Could you describe for me what series is to you?  I've only seen instructions for wiring the resistors is parallel.  We are talking about LED bulbs made to operate on 12VDC aren't we?

kioolt wrote:Could you describe for me what series is to you?  I've only seen instructions for wiring the resistors is parallel.  We are talking about LED bulbs made to operate on 12VDC aren't we?

Ohms law:

series = sum of all resistance in a circuit
parallel = sum of all resistance in a circuit divided by the number of components

That tells me nothing about how to wire it into the circuit.  I need directions like cut the wire and so forth.

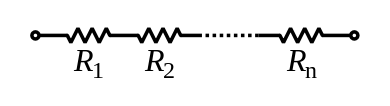Series






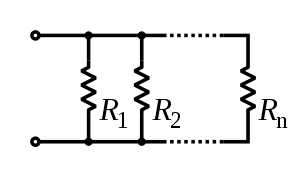Parallel

If you are doing a direct replacement of the incandescent bulbs for LEDs, and still using the same OEM flasher circuitry, then ballast resistors at each signal is not required.  This is a BMW, not a Japanese motorcycle.  Ballast resistors are a stop-gap solution for Far East machines.

The electronics inside the OEM flasher can accommodate the change to LEDs easily. The only alteration you have to make is to disable the hyperflash functionality inside the flasher (blinking the signals at twice their normal rate).  Hyperflashing occurs when the circuit detects a blown signal bulb as evidenced by the reduced current draw.  This change is accomplished by removing the ground on pin 7 of the U243B integrated circuit.  The link I supplied above shows the particular trace to cut.  Cutting the trace will cause the flasher module to not sense the reduced current and try to hyperflash the signal lights.  You signals will function normally again.

You will note that there are two different types of flasher modules for K-bikes. One has through-hole components and a brown circuit card; the other has surface mount components and a green circuit card. Which is yours?

robmack wrote:If you are doing a direct replacement of the incandescent bulbs for LEDs, and still using the same OEM flasher circuitry, then ballast resistors at each signal is not required.  This is a BMW, not a Japanese motorcycle.  Ballast resistors are a stop-gap solution for Far East machines.

The electronics inside the OEM flasher can accommodate the change to LEDs easily. The only alteration you have to make is to disable the hyperflash functionality inside the flasher (blinking the signals at twice their normal rate).  Hyperflashing occurs when the circuit detects a blown signal bulb as evidenced by the reduced current draw.  This change is accomplished by removing the ground on pin 7 of the U243B integrated circuit.  The link I supplied above shows the particular trace to cut.  Cutting the trace will cause the flasher module to not sense the reduced current and try to hyperflash the signal lights.  You signals will function normally again.

i can't see the link

Yes, Look at reply #22 and #23 in that thread.

BTW. ballast resistors _may_ be a way to fool the bulb monitoring unit in the K-bike if you don't want to eliminate the BMU altogether.   The BMU monitors the rear running lights and rear brake lights.  The BMU does not monitor the signal lights, luckily.

robmack,

Isn't the resistance of the LED bulb actually higher then the regular bulb not lower at stated above?  I always though LEDs are suppose to be energy efficient.

tagaz wrote:

robmack wrote:If you are doing a direct replacement of the incandescent bulbs for LEDs, and still using the same OEM flasher circuitry, then ballast resistors at each signal is not required.  This is a BMW, not a Japanese motorcycle.  Ballast resistors are a stop-gap solution for Far East machines.

The electronics inside the OEM flasher can accommodate the change to LEDs easily. The only alteration you have to make is to disable the hyperflash functionality inside the flasher (blinking the signals at twice their normal rate).  Hyperflashing occurs when the circuit detects a blown signal bulb as evidenced by the reduced current draw.  This change is accomplished by removing the ground on pin 7 of the U243B integrated circuit.  The link I supplied above shows the particular trace to cut.  Cutting the trace will cause the flasher module to not sense the reduced current and try to hyperflash the signal lights.  You signals will function normally again.

i can't see the link

Thanks Guys, I will give this a go and let you know what happens 

Here's and explanation I copied from an internet resource for my own reference collection. I don't recall the original source.


"An LED (the diode component) is not a resistive device. Once a diode reaches its threshold voltage, it "turns on" and the effective resistance of the device is essentially zero. 

Because of this, LED devices typically have a resistor in series with the diode. When the diode resistance goes to zero, the resistor determines the current in the circuit. This limits the current that flows through the diode to keep the diode from burning out. 

So, what you have in your torch bulb is an LED in series with a 300 ohm resistor. when the LED turns on, its resistance goes to zero, the total resistance is 300 ohms, which limits the current to 10 mA. At 3V, your total power consumption is 30 mW. 

For the amount of light the LED generates, this is still significantly more efficient than an incandescent bulb. (a 10 W LED bulb generates about the same amount of light as a 65 W incandescent, and there's a lot less wasted heat.)"

The description for the LED you found is correct.  The problem with applying it to the bulbs sold for use as turn signal bulbs is that the series resistor is already built into the bulb.  The LED description you found is for one that you would go down to radio shack and buy in one of their blister packs and built your own circuit.  The resistance of LEDs turn signal bulbs is actually high because of the built in series resistor.

kioolt wrote:robmack,

Isn't the resistance of the LED bulb actually higher then the regular bulb not lower at stated above?  I always though LEDs are suppose to be energy efficient.

As Tagaz correctly pointed out, this is not strictly true. because LEDs are active semiconductor components and not simply resistors, like an incandescent bulb.  

LEDs offer low impedance to current flowing in one direction, and high impedance to current flowing in the opposite direction.  A LED lights when the current flows in the forward direction through the device from its anode to its cathode.  The amount of current drawn by a LED is very small ...  about 20mA.  There is a very slight voltage dropped across the LED, about 1.2V - 2.4V, when lit.  It's the low current draw that makes LEDs seem like they are low resistance.  Ohms Law states R = E/I, where I = 0.02A and E = 2.4V.  Therefore R = 120 ohms.  That's low resistance.  

However, if you were to apply 12V across a normal LED, it would blow up. Its 120 Ohm resistance would attempt to draw 12V/120 = 0.1A (100mA).  Therefore you have to have a series resistor to limit current.  The resistance of the LED (120 ohms) plus the series resistance (470 Ohms) makes the combination seem high.

Does that make sense?

But isn't the series resistor for turn signal LEDs built into the bulb?

AndrewP wrote:
Hi Rob,

I did see this but its waaaayyyyyyyy out of my league 

Andrew

No problems, Andrew. We'll guide you through the process step by step. See whats inside your flasher module first (see my posting above ... through-hole or SMD).

kioolt wrote:But isn't the series resistor for turn signal LEDs built into the bulb?

Correct, it is.  That's what I confirmed.  If you measured the resistance of a 12V LED sold for automotive use, in one direction it would show infinite ohms and in the other about 500 ohms.

If you have a modern multimeter with a "Diode" setting, the meter will indicate the reverse resistance and the forward voltage drop. Much more useful than a bog standard ohm meter.

So, the effective operating resistance is higher because the current is lower.

the only led mods i have done were a few yrs back. 
and those led turn signal bulbs &  tail/stop bulbs had no built in resistors.
i do recall seeing the ones you speak of when i was in town trying to find a bulb for the front park light/eyebrow light.
i may have to give 'em a try.

My training in electronics began when computers ran on valves/tubes.
And one of my favorite rules/laws was "Moore's Law".
Which states, " Technology will double every six months".
Moore's Law became extinct some time ago.
Nowadays it can double at anytime.

I got my degree in industrial electronics in 1976.  Did you get my PM or did I not complete all the necessary steps to send it?

robmack wrote:

AndrewP wrote:
Hi Rob,

I did see this but its waaaayyyyyyyy out of my league 

Andrew

No problems, Andrew.  We'll guide you through the process step by step.  See whats inside your flasher module first (see my posting above  ... through-hole or SMD).

Ok too easy, oil and filter change completed now onto my favourite " electrics " will open up relay and cut to pin 7 and try connecting the LED'S again : )  let you know hoe I go

kioolt wrote:I got my degree in industrial electronics in 1976.  Did you get my PM or did I not complete all the necessary steps to send it?

pm rcvd & replied

Load resistors are a kludge. (And they generate heat which usually isn't a problem but can be if you're unlucky.)

Much easier and better just to cut Pin 7 in the flasher relay.

http://www.kbikeparts.com/classickbikes.com/ckb.tech/0.ckb.tech.files/ledoemflrelay/ledoemflrelay.htm

robmack wrote:

AndrewP wrote:
Hi Rob,

I did see this but its waaaayyyyyyyy out of my league 

Andrew

No problems, Andrew.  We'll guide you through the process step by step.  See whats inside your flasher module first (see my posting above  ... through-hole or SMD).

Ok Flasher relay out and popped off the casing and this is how mine looks

Just cut that small trace between the pin and that large copper island. Don't nick any of the other traces.

In the future, if you want to restore the circuit back to stock, it's an easy fix to solder a small wire across the cut trace, bridging the pin with ground again.

robmack wrote:

Just cut that small trace between the pin and that large copper island.  Don't nick any of the other traces.

In the future, if you want to restore the circuit back to stock, it's an easy fix to solder a small wire across the cut trace, bridging the pin with ground again.

YOU ARE A LEGEND !!  Worked a treat    

Glad to hear it worked. Enjoy!

kioolt wrote:That tells me nothing about how to wire it into the circuit.  I need directions like cut the wire and so forth.

Just wire the resistor in line with the hot going to each lamp individually.

Hello! I was having the same issue with my led blinkers as described of most of you in this thread. So I followed your advice to “cut a leg” on the microprocessor and now it works perfect! Thank you!

The thing is that when I opened the relay box I unfortunately hit one of the condensators on the card so bad it fell off. See picture.

The blinker function still works perfect so now I wonder what the condensatior is for and if I need to repair it.

Best regards
Martin

https://i.servimg.com/u/f80/20/05/64/87/ed61ca10.jpg

Conductor may be the right word for the component. 😁

likely means capacitor

in some cases the capacitor function is just to smooth the power ( Positive supply ) going to some components

Thanks for the wealth of knowledge. This has been great and to find and I’m about to proceed with the cut. However I found a point that looks burnt out. Does anyone know what this is And whether I should solder it up before I pack it up? The bike was working when I took it apart but don’t want to miss anything while I’m putting it back together. Cheers

Looks like at some pint in the bike's life there was a short in the dash wiring.  Excess current was drawn through the relay contacts and burnt the PCB which couldn't handle the current.  The board appears to have been reworked at some point also.  There is burnt flux around many of the contacts towards the edge of the card.  I'd first clean up the board using isopropyl alcohol and a brush.  Then once clean, resolver the relay contact. Check that none of the traces are burnt through.  Then you can probably put the module back in service.